The density triangle is a fundamental concept in physics and chemistry that illustrates the relationship between mass, volume, and density. This triangle serves as a useful tool for students and professionals alike in various fields, including science and engineering. By understanding how these three variables interact, one can solve a variety of problems related to materials and their properties. In this article, we will delve deep into the density triangle, exploring its significance, applications, and how to utilize it effectively in calculations.
In the next sections, we will break down the components of the density triangle, including definitions and formulas, and provide practical examples to demonstrate its application. Additionally, we will discuss the importance of density in real-world scenarios, such as material selection in engineering and its role in everyday life. Whether you are a student studying for an exam or a professional seeking to refresh your knowledge, this article aims to provide comprehensive insights into the density triangle.
Furthermore, we will look into common misconceptions surrounding density and how to avoid them. By the end of this article, you will have a solid understanding of the density triangle and be equipped with the knowledge to apply it in various contexts. Let’s get started!
Table of Contents
- 1. Overview of the Density Triangle
- 2. Components of the Density Triangle
- 3. The Density Formula
- 4. Calculating Density Using the Triangle
- 5. Applications of Density in Real Life
- 6. Common Misconceptions About Density
- 7. Conclusion
- 8. Call to Action
1. Overview of the Density Triangle
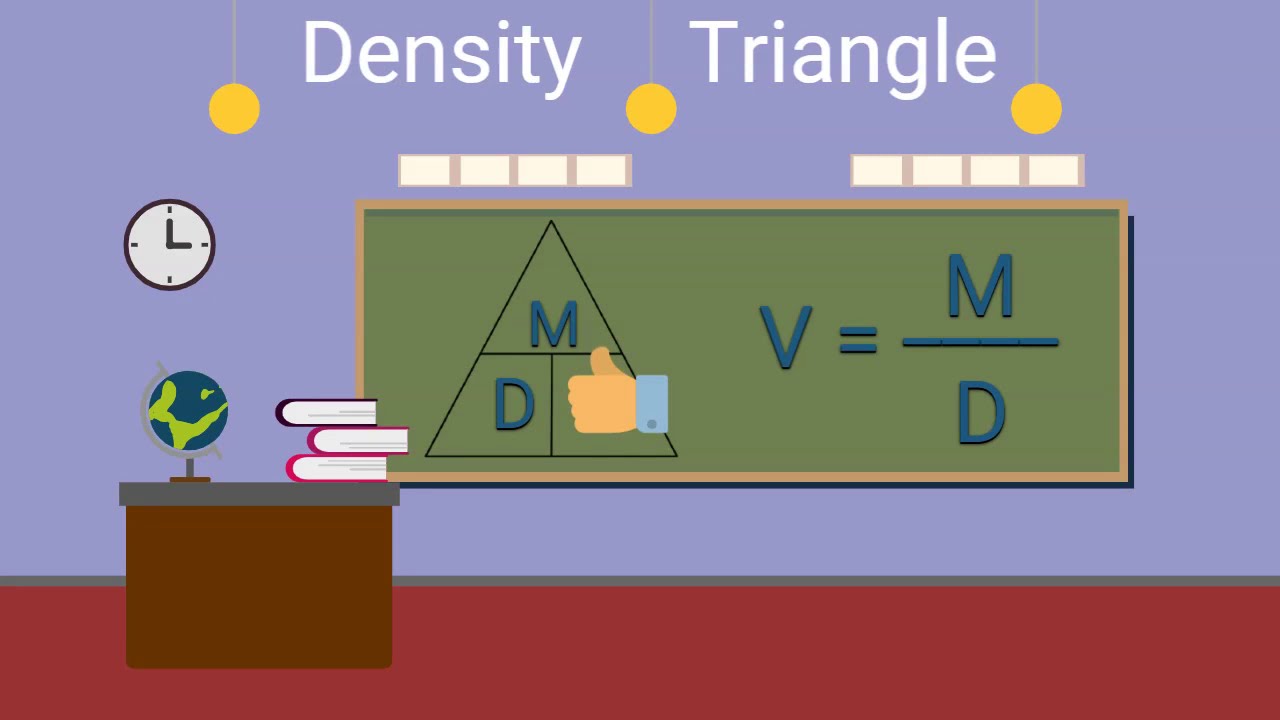
The density triangle visually represents the relationship between mass, volume, and density, which are interconnected properties of matter. In this triangle, each corner represents one of these properties:
- Mass (m): The amount of matter in an object, typically measured in grams (g) or kilograms (kg).
- Volume (V): The amount of space occupied by an object, usually measured in liters (L) or cubic meters (m³).
- Density (D): The mass per unit volume of an object, expressed as D = m/V.
2. Components of the Density Triangle
To effectively use the density triangle, it’s essential to understand its components:
2.1 Mass
Mass is a measure of the quantity of matter in an object. It is not dependent on the object's location and remains constant regardless of gravitational forces. In the density triangle, mass is typically represented at the top point.
2.2 Volume
Volume refers to the three-dimensional space occupied by an object. It can vary depending on the object's shape and state (solid, liquid, gas). In the triangle, volume is represented at the bottom left corner.
2.3 Density
Density is defined as mass per unit volume (D = m/V). It provides insight into how compact or concentrated an object is. In the density triangle, density is represented at the bottom right corner.
3. The Density Formula
The density formula is derived from the density triangle and is expressed as:
D = m/V
Where:
- D = Density
- m = Mass
- V = Volume
This formula allows you to calculate any of the three properties if the other two are known. For example, if you know the mass of an object and its volume, you can easily determine its density.
4. Calculating Density Using the Triangle
Using the density triangle to calculate mass, volume, or density involves rearranging the formula accordingly:
- To find Density (D): D = m/V
- To find Mass (m): m = D × V
- To find Volume (V): V = m/D
Let’s look at a practical example:
If you have a block of metal that weighs 200 grams and occupies a volume of 50 cubic centimeters, you can calculate its density as follows:
D = m/V = 200 g / 50 cm³ = 4 g/cm³
5. Applications of Density in Real Life
Density plays a crucial role in various applications across multiple fields:
- Material Selection in Engineering: Engineers often use density to select appropriate materials for construction and manufacturing, ensuring structural integrity and performance.
- Buoyancy: Understanding density is vital in determining whether an object will float or sink in a fluid. This principle is applied in shipbuilding and designing aquatic vehicles.
- Food Industry: Density measurements can help in quality control processes for food products, ensuring that they meet specific standards.
- Environmental Science: Density is used in assessing pollutant concentrations in water and air, aiding in environmental protection efforts.
6. Common Misconceptions About Density
Several misconceptions surround the concept of density:
- Misconception 1: Heavier objects always have a higher density.
Reality: Density depends on both mass and volume. An object can be heavy but have a large volume, resulting in lower density. - Misconception 2: All liquids have the same density.
Reality: Different liquids have different densities, which is why oil floats on water. - Misconception 3: Density only applies to solids.
Reality: Density applies to all states of matter, including liquids and gases.
7. Conclusion
In conclusion, the density triangle is an invaluable tool for understanding the relationship between mass, volume, and density. By mastering this concept, individuals can apply it effectively in various real-world scenarios, from engineering to environmental science. Understanding the components and calculations associated with the density triangle empowers you to make informed decisions based on material properties.
8. Call to Action
We invite you to leave your thoughts or questions in the comments below. If you found this article helpful, please share it with others who may benefit from understanding the density triangle. For further reading, check out our other articles on related topics!
Thank you for visiting our site, and we hope you return for more insightful content!